Sand Box: Construct and evaluate magnitude-rate distribution scenarios
The magnitude-rate distribution (MRD) of many large faults and subduction zones does not follow typical Gutenberg-Richter (GR) distributions. Often, the rates of occurrences of large-magnitude earthquakes, estimated based on historical or paleoseismic data, tend to be higher than what is implied by GR distributions that define the MRDs of small and intermediate-magnitude earthquakes. Seismologists often use the concept of characteristic-earthquake (ChE) to formulate MRD of faults and subduction zones (FSZ) with complex seismicity. In a ChE model, it is assumed that FSZ release large portions of their seismic energy by large earthquakes characteristic of the FSZ’s rupture areas and conditions.
Consider a fault with rupture length and width of \(L\) and \(W\), respectively, accumulating strain within its rupture area with the slip rate of \(S\) mm/year. Seismic moment rate is calculated as
$$M_0=\mu*L*W*S…(1)$$
Where \(\mu\) is the shear modulus of rocks near the rupture area. The task of building a seismicity model is to formulate an MRD for all probable earthquakes on the fault so that they collectively release the estimated accumulating seismic moment rate \(M_0\). Typically, the MRD is formulated using a simple GR distribution if there is no info on the rates of occurrences of small and/or intermediate magnitude earthquakes to constrain the MRD. However, the situation is more complex when related historical and instrumental earthquake recordings, geodetic, and/or paleoseismic data for the fault or group of faults need to be acknowledged. Such information constrains the MRD construction, often resulting in a more complex model than a typical GR distribution.
Figure 1 shows MRD for a fault scenario with \(L=120\) km, \(W=12 \)km, and \(S=5\) mm/year. Given the rupture area of the fault, the maximum probable magnitude of the fault is set as \(M = 7.5\). The occurrence rate of \(M \ge 5.0\) is constrained as 0.1, assuming that the fault has experienced about 10 \(M \ge 5.0\) earthquakes within the last 100 years. The blue line in Figure 1 represents a GR distribution that matches the given info on the occurrence rate of \(M \ge 5.0\) and the upper bound magnitude for the fault.
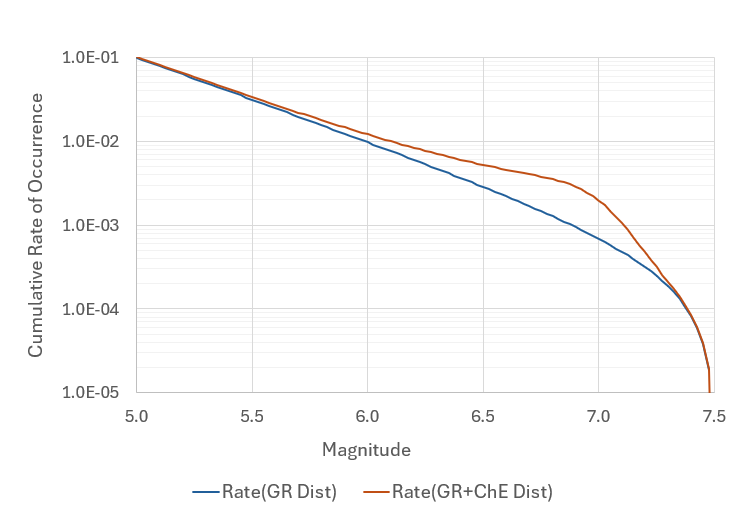
Figure 1. MRD for a hypothetical fault scenario with \(L=120\) km, \(W=12 \)km, and \(S=5\) mm/year with the occurrence rate of \(M \ge 5.0\) as 0.1. The GR distribution only releases about \(55\%\) of the accumulating seismic moment rate. The release of the leftover moment rate is formulated using a ChE model, red line.
It should be noted that the GR distribution is constructed using \(b=1.0\); see the link on GR distribution on the previous page for a more detailed discussion on the subject. The GR distribution in Figure 1 only releases about 55% of the total available seismic moment rate. The leftover seismic moment rate is released by a range of characteristic earthquakes, defined by a Gaussian distribution with a mean of \(M_{Ch}=7.0\) and \({\sigma}_M = 0.24\), only considering two standard deviations to capture the variation.
In practice, the upper bound magnitude for the GR distribution is often considered lower than the ChE upper bound magnitude. Figure 2 shows a different MRD for the fault scenario in Figure 1, using the GR upper bound magnitude of \(M=7.0\). The GR earthquakes in Figure 2 release only 30% of the total seismic moment rate. The rest is released by the characteristic earthquakes, which result in higher occurrence rates for large earthquakes than those shown in Figure 1.
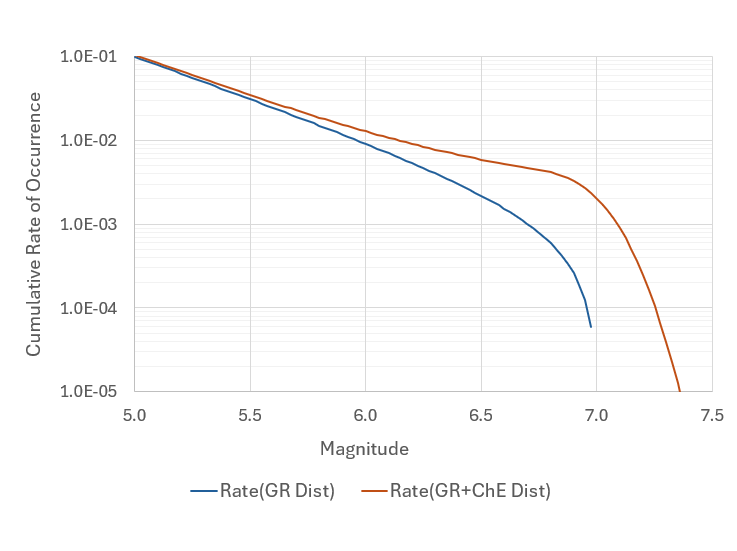
Figure 2. A plot of MRD for the fault scenario described in Figure 1, but using \(M=7.0\) as the GR upper bound magnitude. The Lower upper bound magnitude for GR, compared to that of Figure 1, is used to limit the magnitude overlap of GR and ChE distributions. The GR distribution releases about \(30\%\) of the total seismic moment. This results in higher rates of large-magnitude earthquakes than those in Figure 1.